View this project’s code on GitHub :)
Background
Quantum Computing
Qubits
The most basic unit of information in classical computing is the bit. It stores a value either of 0 or 1, which represent the presence or absence of electrons in a transistor.
In quantum computing, however, the most basic unit of information is the qubit. A qubit, like a bit, can store either 0 or 1, but it also has the unique ability to store a value that is both 0 and 1: a superposition state.
Each of these superposition states can be represented by a point on the surface of the bloch sphere:
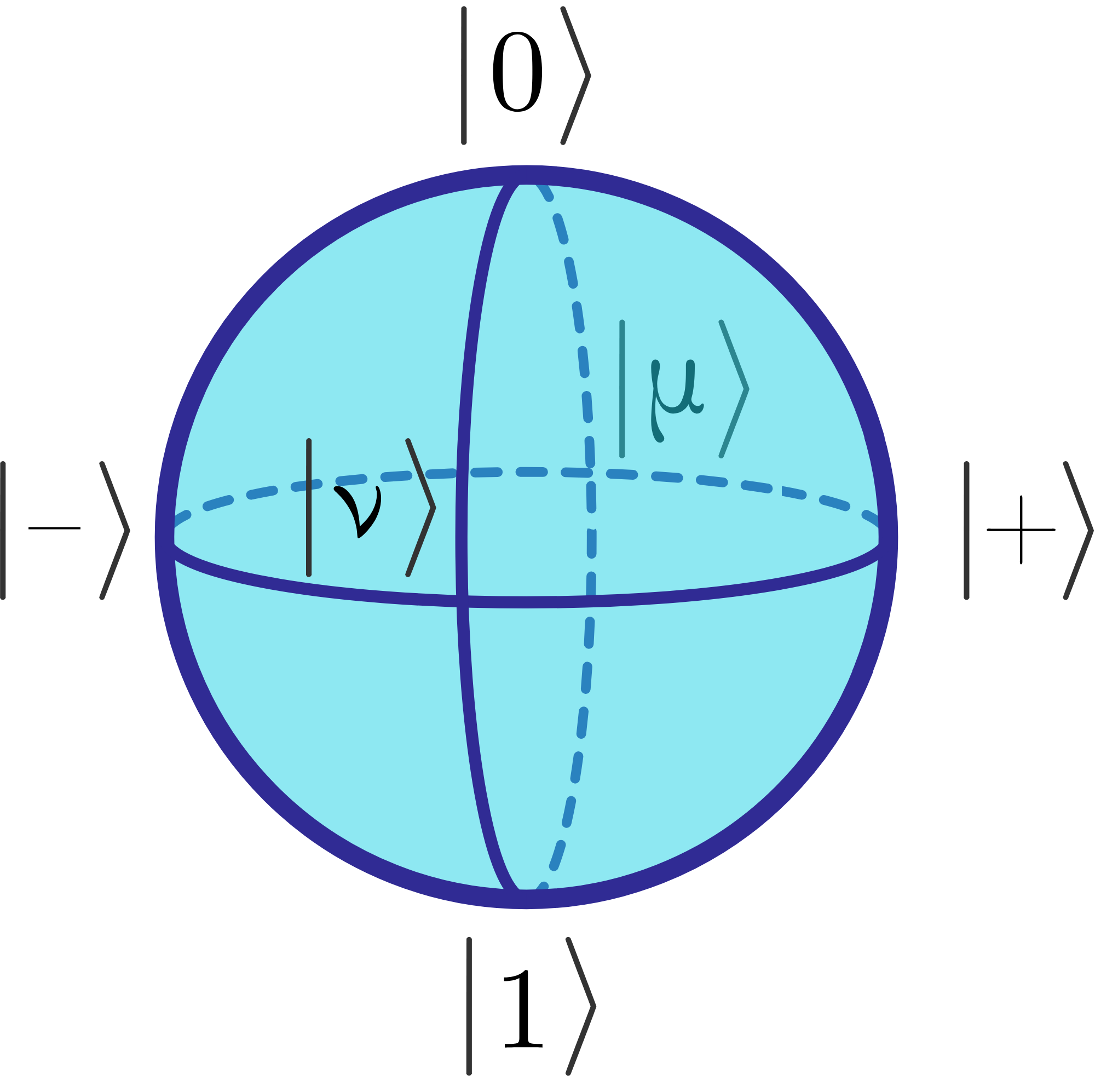
Image from Brilliant
For reference, the horizontal axis between |-〉 and |+〉 will be referred to as the x-axis, the vertical axis will be referred to as the z-axis, and the axis running between |µ〉 and |ν〉 will be referred to as the y-axis.
The classical-like states |0〉 and |1〉 are shown at the top and bottom of the bloch sphere. Any superposition between zero and one would fall somewhere on the surface of the sphere between these two points. While there are technically infinite superposition states (there are infinite points on any surface), the only states referred to here will be |0〉 and |1〉, |+〉, and |-〉. When a qubit in superposition is measured, it collapses into either the |0〉 state or the |1〉 state. The probability of either outcome is determined by the superposition, and when the state collapses, all information about the superposition state is lost.
Quantum Gates
In classical computing, logic gates are used to perform operations on bits. These include gates such as not, which flips that value of a bit, and, which outputs a bit with value 1 if both of it’s inputs are 1, or, which outputs 1 if either input is 1, and several others.
Note that the not gate is the only classical logic gate that acts on only a single bit; every other gate requires at least two bits as input.
In quantum computing, due to the more complex nature of qubits, there are many single qubit logic gates. Those described here are by now means an exhaustive list; rather, they are simply the set of gates necessary for this research. Each of these single-qubit gates can be thought of as a rotation on the bloch sphere.
(More information about quantum gates can be found on the IBM quantum operations glossary, but even this is not a complete list.)
The first quantum gate needed for this research is the quantum not gate, also sometimes called the X gate. This gate functions much like the classical not gate, flipping a qubit in the |0〉state to a the |1〉 state and vice versa. This gate is analogous to a rotation around the horizontal axis. Since the superposition states |+〉 and |-〉are on the axis of rotation, they are unchanged by this gate.
The second quantum gate is one of the most important gates in quantum computing: the hadamard, or H gate. This gate is used to induce superposition: it maps |0〉 to |+〉 and |1〉 to |-〉 and vice versa. This is equivalent to a rotation around the line x=z. The states |+〉 and |-〉 both represent a 50/50 chance of getting either a 0 or a 1 when the qubit is measured.
The final single-qubit quantum gate that will be mentioned here is the Z gate. The Z gate is equivalent to a rotation around the z-axis, and it maps |+〉 onto |-〉 and |-〉 onto |+〉. Since |0〉 and |1〉 are on the axis of rotation, they are unaffected by the Z gate.
Something important to keep in mind about the gates mentioned here is that they are all reversible: apply them twice in a row, and the qubit will return to its original state. In fact, this applies to nearly every single-qubit quantum gate.
Entanglement
Now that we’ve discussed superposition and quantum gates, it’s time to talk about entanglement. This is quite a complex topic, so bear with me.
Let’s start off simple: how do we describe the state of two qubits at once? Let’s say we have to qubits, both in the |0〉 state. The joint state, a way to describe both qubits together as a system, can be written using the tensor product:
Next, let’s talk about the |+〉 state. Remember: this represents a 50/50 chance of seeing either 0 or 1 when the qubit is measured. Another way we can write this is:
The coefficients before each state denote the square root of the probability of measuring that state, so a 0.5 probability is shown with the coefficient 1 over the square root of 2.
It is usually convention to normalize the coefficients of a state so that, when squared, they add up to 1, but this isn’t necessary to mathematically define a state. Let’s say we have two qubits, each in some aribitrary superposition state:
and
To write the joint state of these two qubits, we use the tensor product:
The tensor product can be distributed in the same way as integer multipliaction, giving us
However, this is a little confusing. It’s hard to tell how many qubits this joint state is referring to, and hard to understand in general. To simplify, we can write the joint state of two qubits
as
Much nicer! It’s obvious that this is referring to two qubits: there are two numbers inside the ket (the vertical bar and angle brace), and it’s much cleaner looking over all. Using this convention, our two arbitrary superpositions can be written as
This is much easier to understand. We can see that this expression refers to two qubits, since there are two numbers in each ket, and we can see that there are four possible outcomes when the joint system is measured, since there are four terms being added.
Now, consider the joint state
What’s interesting about this state is that unlike the other arbitrary state we looked at, which can be split back up into two separate single-qubit expressions joined by a tensor product, this state cannot be split. We know that it refers to two qubits since there are two numbers in the kets, but there aren’t enough terms to split this up. What does this mean??
This is entanglement! We’re finally here! Entanglement is simply the name given to joint states that, like this one, can’t be split up to refer to individual qubits.
Superdense Coding
Annnndd just like that, we’re moving on again. Now that we’ve talked about entanglement, we can finally talk about superdense coding, the focus of this research! Yay!
The goal of superdense coding is to store 2 bits of information in a single qubit, and still be able to extract that information again afterward. It’s easy enough to store a lot of information in a qubit: a point on the sphere can be defined using two rotations of variable size, which can each have infinite decimal places and therefore store infinite bits. However, this information would be nearly impossible to extract. For one thing, since a measurement of a qubit gives either a 1 or a 0, we can only converge on the values of the rotations over time with repeated measurements; it would take infinite measurements to determine them exactly.
But the bigger problem is this: when we measure a qubit, it collapses. Every time we measure it after that, we will always get the value we measured the first time. For us to make a large number of measurements, we need to prepare a large number of qubits in the same state. When we know exactly what the state is, this isn’t the easiest thing to do (but it is possible). However, when we don’t know what state the qubit is in, such as when someone sends it to as as part of a communication, creating the qubit again from scratch is impossible.
Why, you may be asking, can’t we just make copies of the qubit, and measure those? Why would we have to recreate it from the beginning? The answer to that question is the quantum no-cloning theorem. The quantum no-cloning theorem states that for a pair of qubits, one in the state |0〉 and one in some arbitrary state |ψ〉, there exists no series of gates that results in two qubits, both in the state |ψ〉.
To "briefly" explain why, let's look at some hypothetical circuit COPY that could copy the states.
(This is just a bunch of math, so if you'd rather just take my word for it that we can't clone qubits, feel free to skip this explanation and keep reading.)
If we write our aribtrary state |ψ〉 as α|0〉 + β|1〉, we can expand our circuit
like so:
and then further to:
But! We can also expand |ψ〉 first and then apply copy to each of the components:
Distributing COPY gives us:
And finally we simplify:
If the COPY circuit was possible, these two final equations would be equal, so let’s set them equal to each other:
For these two expressions to be equal, we can see that α2 must be equal to α, β2 must be equal to β, and αβ must be equal to zero. All of these conditions are only met when either α=1, β=0 or α=0, β=1. If you take a closer look at what those coefficients would do to the states, you might notice something: the two possible conditions represent the two classical-like states, |0〉 and |1〉.
What this means for our COPY circuit is that it will only ever work on a qubit that is in one of the classical-like states, so unfortunately we can’t copy any arbitrary state.
The upshot of this all is that we can’t make use of the rotations or coefficients in a quantum state to store many classical bits, because we can’t extract them again afterward. The aim of superdense encoding is to store two classical bits in a single qubit. To do this, we’ll have to find some other method of storing data in a quantum state.
The Bell State
In the last section, we saw the arbitrary entangled state
Much like
is an arbitrary form of the |+〉 state,
is an arbitrary form of the Bell State. The Bell State is the simplest entangled quantum state, and it looks like this:
You might notice that this looks very similar to the |+〉 state, and you’d be correct! The |+〉 state has a 50/50 chance of being measured as 0 or 1, and when measured, the Bell State has a 50/50 chance for either both qubits to be measured as 0, or both to be measured as 1. This will make more sense when we look at how the State is constructed with gates.
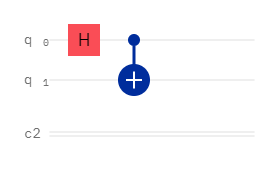
We start off with a Hadamard gate, which takes us from the state |00〉 to the state
Then, we apply a new gate. The controlled not gate, or CX gate, is the first (and only) two qubit gate mentioned here. Luckily, it’s faily simple. It functions as the X gate if the control qubit (in this case, the first qubit), is in the state |1〉, and does nothing if the control qubit is in the state |0〉.
But wait! The control qubit isn’t in the |1〉 state or the |0〉 state when we apply the CX gate, it’s in the |+〉 state! What happens now??
The answer is entanglement. When measured, the first qubit will either be in the state |0〉, in which case the CX gate wouldn’t have acted and the second qubit would also be |0〉, OR the first qubit will be in the state |1〉, in which case the CX would have acted, and the second qubit will also be in the the |1〉 state. However, up until we measure the system, we can’t know what state either qubit is in, and we can’t talk about them separately, since the second qubit depends on the first!
Alright, let’s really dig into superdense coding now. Let’s say that our two friends of cryptography fame, Alice and Bob, are in the same physical location. Let’s say that they prepare two qubits in the Bell State, and each take one of the qubits physically. Alice and Bob then go home to their separate houses with separate quantum computers.
Encoding Information in Alice’s Qubit
Alright. How do we encode information into Alice’s qubit (and by extension, the joint entangled state)?
If we wanted to encode a 1 in a classical bit, we would use a not gate to flip it from the 1 state to a 0 state. So let’s try applying the quantum not gate–the X gate–to Alice’s qubit.
Since the X gate only acts on one qubit, it will flip the value of the first qubit in each ket of our Bell state, giving us
Since addition is commutative, we can change around the terms a bit to get
This isn’t a necessary step, but it helps with following the process. Now, since we’ve changed the joint state by applying the X gate to Alice’s qubit, technically we’re halfway there! We’ve encoded a bit of information. But let’s not forget our goal here: how can Bob extract this bit of information?
For Bob to be able to measure anything, he’ll need both qubits; otherwise, he only has part of an entangled state. So let’s say Alice physically sends her qubit to Bob. (Important note: this is secure communication, since anyone who would intercept Alice’s sent qubit would only be able to see part of an entangled state, and, like Bob, who without both qubits can’t measure anything, they would be unable to glean information from it.) Now Bob has both qubits: what can he do to extract the bit Alice encoded?
Well, if the CX gate entangled the qubits, and quantum gates are reversible, maybe we can use it again to unentangle the qubits? Let’s give it a shot. Since in the first term, the control qubit (Alice’s qubit and the number listed first in each ket) is a 0, the CX gate will have no effect: remember, it only flips the target qubit when the control qubit is in state |1〉. However, in the second term, the control qubit is in state |1〉, so we flip the target qubit (Bob’s qubit and the number listed second in each ket). This results in the state:
You may notice that we can now split this state up by un-distributing the tensor product: since the state of Bob’s qubit no longer depends on Alice’s, it can be separated out, which would give the state
which can also be written as
Hey! The second qubit ended up in the |1〉 state, which means that no matter what, when Bob measures it he’ll get a 1! Is that the bit Alice encoded? What would have happened if she hadn’t applied the X gate (encoding a 0 instead)?
We start in the Bell State:
Then, after Bob gets it, we apply the CX gate giving us
or
Yes! The second qubit is now in the |0〉 state! We did it! Ok, so Alice can encode information by choosing to apply or not apply an X gate to her qubit before sending it to Bob, and Bob can extract that information by unentangling the qubits and measuring his! Wonderful. But what about the second bit? Superdense coding promised two classical bits in a qubit, and so far we only have one!
Relative Phase
To encode the second bit, we need to talk about relative phase. Relative phase is the difference between
and
Let’s take a look at our Bell state, but with the opposite relative phase:
Were Bob to decode this with his CX gate, he would get the joint state
or
Hey! That’s different than the previous final state we got, which was
The Second Bit
If we changed something about the state, and didn’t affect the second qubit at all, then we’ve done it! We’ve encoded the second bit. But how do we change the relative phase to do this encoding?
The answer: we use the Z Gate.
So this means that we’ve successfully encoded both bits of information, and we know how to extract one, but how do we extract the other? Remember, |+〉 and |-〉 both have a 50/50 change of being measured as 0 or 1, so we can’t determine the difference between these two states with only measurement.
Is there some way we can determine the difference?
Luckily for us, the Hadamard Gate is exactly what we need. Remember, it converts |+〉 to |0〉 and |-〉 to |1〉, allowing us to differentiate between them.
Final Protocol
Now that we have a method for encoding and decoding both of our bits, we’ve got our final protocol for superdense coding with the Bell state:
-
Alice and Bob start with entangled qubits in the Bell State
-
Alice encode her desired two-bit message:
- 00: no gates
- 01: X gate
- 10: Z gate
- 11: Z and X gates
-
Alice physically sends her qubit to Bob
-
Bob applies a CX gate on his qubit, using Alice’s qubit as a control, storing the second encoded bit in his qubit
-
Bob applies a Hadamard gate to Alice’s qubit, converting it either from |+⟩ to |0⟩ or from |–⟩ to |1⟩, decoding the first encoded bit
-
Bob measures both qubits
Since all qubits are in classical states at the time of measurement, Bob is guaranteed to get the correct results: Alice’s encoded message! There is no tricky quantum randomness that affects the measurement!
Our final circuit looks like this:
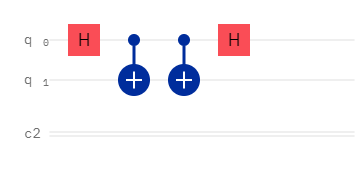
The gates used to encode information would be inserted between the two CX gates.
My Research
Higher Qubit Entangled States
The Bell state is what is known as the maximally entangled state for two qubits. For entangled states with more qubits, there are different kinds of maximal entanglement that can be produced. For example, for three qubits, there are two maximally entangled states, each of which cannot be transformed into the other through unitary gates.
The GHZ State
The first, the GHZ state, is based on the Bell state. The circuit used to create it is very similar:
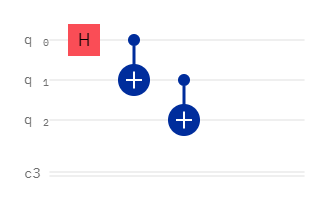
and the state itself is a clear extension of the Bell state:
It’s almost entirely the same, but with an extra qubit in each ket. This also is easily generalized to even higher qubit entanglement: to create the state with one more entangled qubit, simply add another CX Gate, chaining that qubit into the entanglement and adding another number to each of the kets. For example, the 4 qubit GHZ state would be
The W State
The other maximally entangled three qubit state is called the W state. It is based on the joint state created by applying an X gate to the first qubit of the Bell state
and looks like this:
The W state can also be generalized to higher qubit states, but it’s a little trickier. Each added qubit adds a term to the numerator: for example, the four qubit W state would be
The circuit used to create the W state is significantly more complex than that used to create the GHZ state. It requires precise rotations based on an inverse cosine function, which is a function notably lacking from IBM’s quantum circuit coding script, OpenQASM, and uses a controlled Hadamard gate:
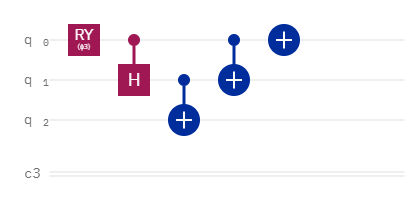 Where ϕ3 is
Where ϕ3 is
This makes using the W state significantly more difficult than using the GHZ state.
Research Goals
The goal of my research is to make use of the 7 qubit composite GHZ-Bell state
to store 7 classical bits in four qubits.
I will then use these 7 classical bits to represent 1 of the 128 ASCII characters, and develop a small secure communication test that sends one character at a time, encoded in the qubits.
Finally, I plan to run this basic version of secure communication on IBM’s 5 qubit qauntum computers, and analyze the amount of error in the decoded messages.
Demo Code
All files referenced here can be found on this project’s github
Two versions of the demo have already been created. The first, demo1.py, which uses the resources in sec_comm_5.py, is based on the original 5 qubit joint state, and makes use of a limited subset of the ASCII character set. It will not be discussed here, although it functions similarly to the second version.
The second version, demo2.py, uses the resources from sec_comm_7.py. It is based on the updated 7 qubit joint state outlined above, and makes use of the entire 7 bit ASCII character set, which contains 128 characters.
The two major parts of the code are the following functions:
- encode()
- get_char()
The other functions in sec_comm_7.py also play important roles, but they are relatively simple compared to the three listed, and are less representative of my own work.
Overview
The qubits that make up the joint GHZ-Bell state will be entangled, encoded, passed through a series of identity gates, decoded, and measured, and then the lone Bell state will go through the same procedure. An important note: the series of identity gates is intended to simulate, to some extent, the passage of qubits through a data cable. The thinking behind this is that decoherence becomes more likely the longer states have to be maintained, so by prolonging the circuit without changing the state of the qubits, the opportunity for decoherence is being increased similarly to how it would be in the case of a qubit traveling along a data cable.
The Encode Function
def encode(char:str, circuit: qiskit.circuit.QuantumCircuit, n: int) -> None:
binary = get_binary(char)
if n == 5:
if binary[0] == '1':
circuit.z(0)
if binary[1] == '1':
circuit.z(1)
if binary[2] == '1':
circuit.x(1)
if binary[3] == '1':
circuit.x(0)
if binary[4] == '1':
circuit.x(1)
circuit.x(2)
elif n == 2:
if binary[5] == '1':
circuit.z(0)
if binary[6] == '1':
circuit.x(0)
The goal of the encode function is to apply the gates that encode classical data into the information carrying entangled group parts. The if n == 5: block runs when the GHZ-Bell joint state is being encoded, and the if n == 2: block runs when the lone Bell state is being encoded.
The n == 2 case uses the encoding method discussed in the background above to encode in the lone Bell state.
The n == 5 case uses the following encoding protocol to encode in the joint GHZ-Bell state:
- Base state (all 0s encoded) -> 00000
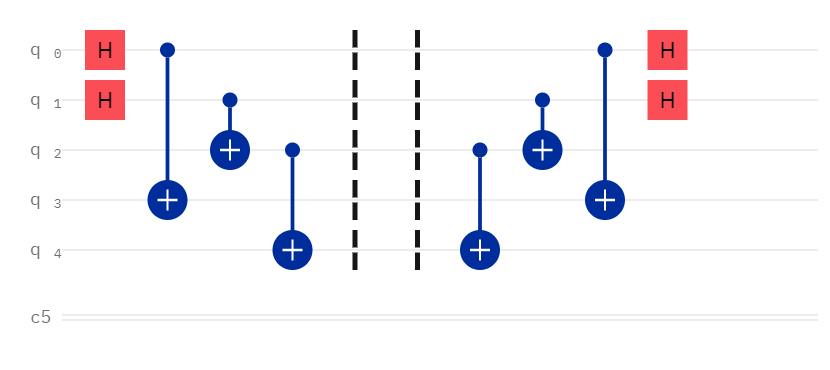
- To encode a 1 in the binary 1s place (
binary[4]), apply an X gate on qubit 1 and qubit 2 -> 00001
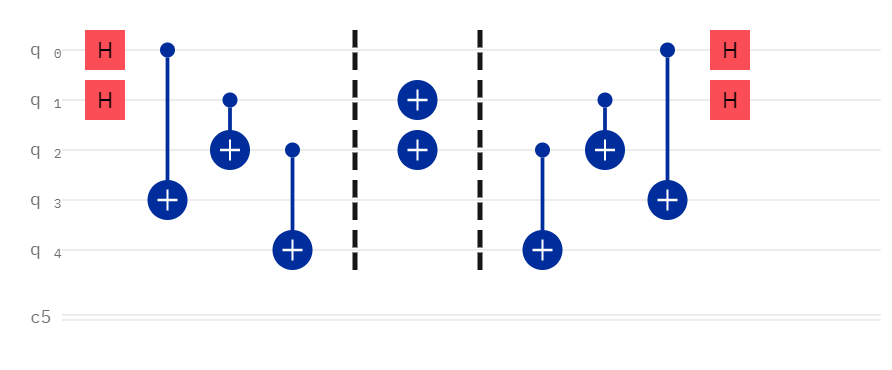
- To encode a 1 in the binary 2s place (
binary[3]), apply an X gate on qubit 0 -> 00010
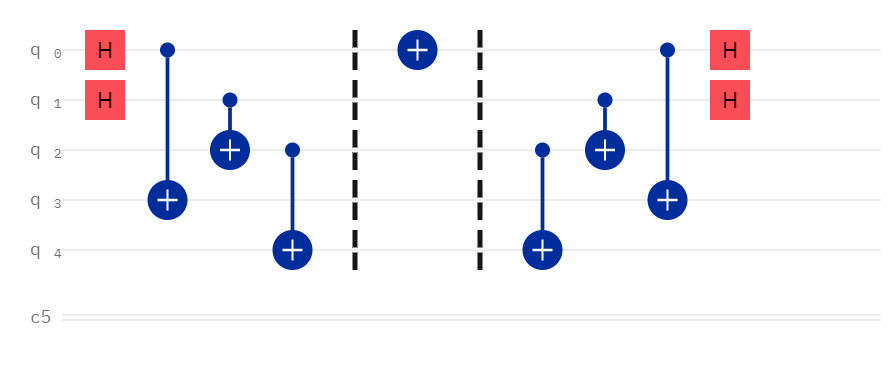
- To encode a 1 in the binary 4s place (
binary[2]), apply an X gate on qubit 1 -> 00100
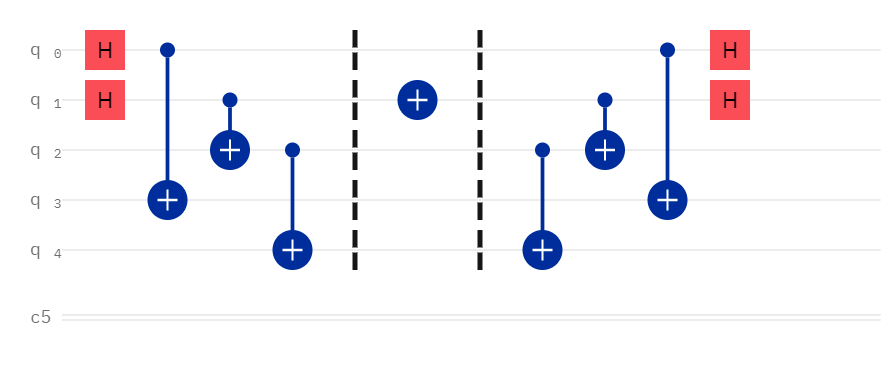
- To encode a 1 in the binary 8s place (
binary[1]), apply a Z gate on qubit 1 -> 01000
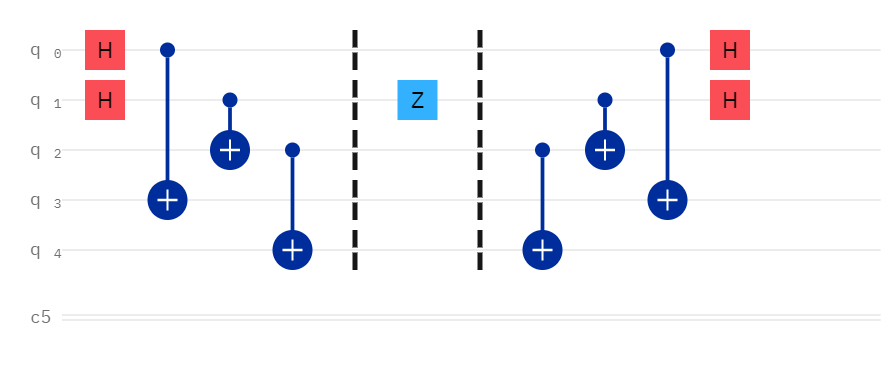
- To encode a 1 in the binary 16s place (
binary[0]), apply a Z gate on qubit 0 -> 10000
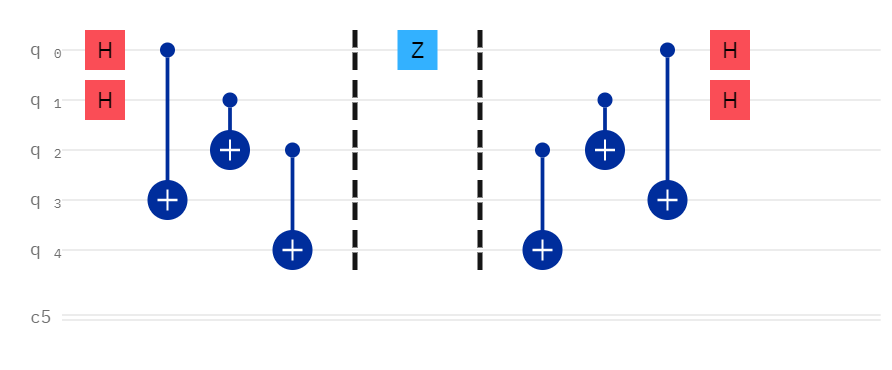
The Decode Function
def get_char(result_counts_5: dict, result_counts_2: dict) -> str:
result_keys_5 = list(result_counts_5)
results_5 = [result_counts_5[i] for i in result_keys_5]
max_val_5 = max(results_5)
index_5 = results_5.index(max_val_5)
key_5 = result_keys_5[index_5]
key_5 = key_5[::-1]
result_keys_2 = list(result_counts_2)
results_2 = [result_counts_2[i] for i in result_keys_2]
max_val_2 = max(results_2)
index_2 = results_2.index(max_val_2)
key_2 = result_keys_2[index_2]
key_2 = key_2[::-1]
key_2 = key_2[:2]
key = key_5 + key_2
int_vers = int(key, 2)
char = chr(int_vers)
return char
The decode function is a little more complex. It uses the dictionaries of results from the pair of circuits representing the joint GHZ-Bell state and lone Bell state returned by IBMQ’s quantum computer to determine what character was encoded.
The first line is creating a list of the keys in the GHZ-Bell circuit’s results dictionary. These are values like '00101', '10000', etc–any five digit binary result that was measured during one of the runs of the circuit. The next line creates a list of the value half of each key value pair, in the same order as the keys list. These are each an integer, representing the number of times that binary key was measured during the runs of the circuit.
Then, the maximum value and it’s index are found using the max() and .index() functions. This gives the index of the most measured key. Using this index, we can access this key, which is stored in key_5. Because of the way information is encoded in the quantum circuits, the key must then be reversed, using string slicing.
The second block of code does the same process, storing the final reversed key for the lone Bell state in key_2.
Finally, the keys are concatenated to create the binary character indicator (stored in key) for the encoded ASCII character. That binary number in base 10 is stored in int_vers, and the chr() builtin function is used to return the actual encoded character as a string.
In combination with the other functions found in sec_comm_7.py, messages can be encoded in quantum circuits, run through IBM’s quantum computers, and decoded on the other side to analyze for error.
Coming Soon: Analyzing Error
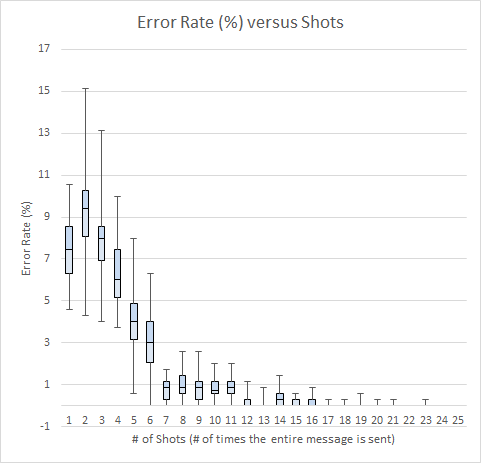
The next steps will be to analyze the error of the quantum systems to determine
- if any specific bits are more prone to errors than others,
- the fewest number of shots required per circuit to maintain low- to no-error results, and
- if the series of identity gates has any effect on the error rate of the messages,
as well as to reach out to experts and confirm that the methods used here are applicable to future hypothetical quantum communication networks.
Data from item (2) above:
Circuit used for item (3) above:

Preliminary data from item (3) above:
Histogram with increasing number of bins, showing distribution of errors per 20,000 for all qubits
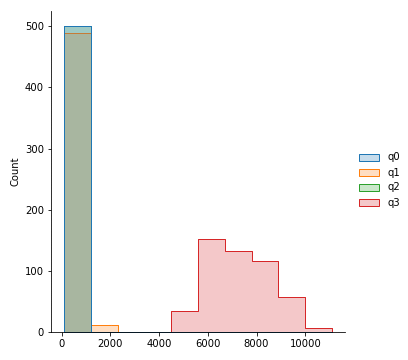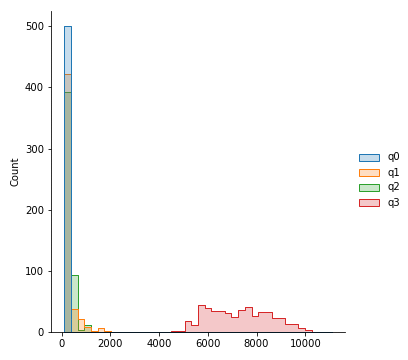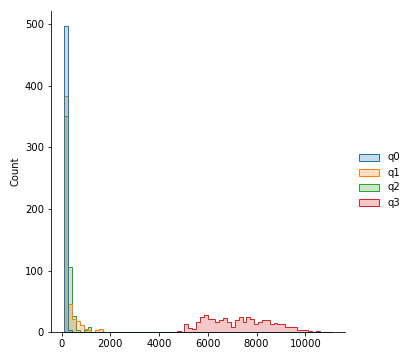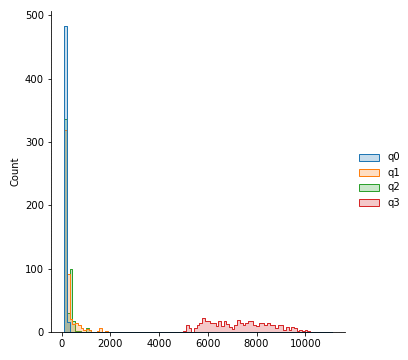
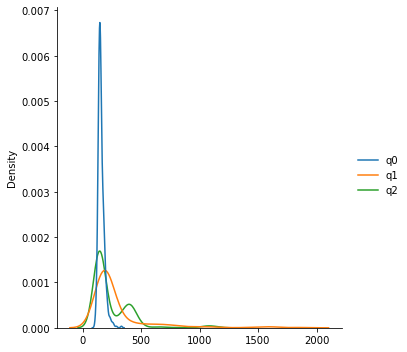
Guassian smoothed distribution for qubits q0 through q2
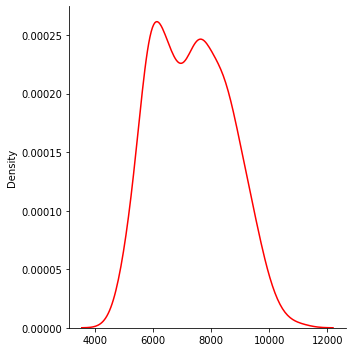
Gaussian smoothed distribution for qubit q3
This page is in progress: it will be updated and progress reports will be added as these steps are completed, and will be replaced by a more cleanly formatted version once all data is collected.
Sources
Abeyesinghe, A., Hayden, P., Smith, G., & Winter, A. J. (2006). Optimal Superdense coding of entangled states. IEEE Transactions on Information Theory, 52(8), 3635–3641. https://doi.org/10.1109/tit.2006.878174
Deng, F.-G., Long, G. L., & Liu, X.-S. (2003). Two-step Quantum Direct Communication Protocol using the einstein-podolsky-rosen pair block. Physical Review A, 68(4). https://doi.org/10.1103/physreva.68.042317
Herbert, S. (2020). Increasing the classical data throughput in quantum networks by combining quantum linear network coding with superdense coding. Physical Review A, 101(6). https://doi.org/10.1103/physreva.101.062332
Learn quantum computing on brilliant. Brilliant. (n.d.). Retrieved October 15, 2021, from https://brilliant.org/courses/quantum-computing/.
Li, J., Song, D. J., Li, R., & Lu, X. (2013). A quantum secure direct communication protocol based on four-qubit cluster state. Security and Communication Networks, 8(1), 36–42. https://doi.org/10.1002/sec.711
Long, G. L., & Liu, X. S. (2002). Theoretically efficient high-capacity quantum-key-distribution scheme. Physical Review A, 65(3). https://doi.org/10.1103/physreva.65.032302
Muralidharan, S., & Panigrahi, P. K. (2008). Perfect teleportation, quantum-state sharing, and superdense coding through a genuinely entangled five-qubit state. Physical Review A, 77(3). https://doi.org/10.1103/physreva.77.032321
Operations glossary. IBM Quantum. (n.d.). Retrieved October 15, 2021, from https://quantum-computing.ibm.com/composer/docs/iqx/operations_glossary.
Saha, D., & Panigrahi, P. K. (2011). N-qubit quantum teleportation, information splitting and superdense coding through the composite ghz–bell channel. Quantum Information Processing, 11(2), 615–628. https://doi.org/10.1007/s11128-011-0270-x
Zhang, W., Ding, D.-S., Sheng, Y.-B., Zhou, L., Shi, B.-S., & Guo, G.-C. (2017). Quantum secure direct communication with Quantum Memory. Physical Review Letters, 118(22). https://doi.org/10.1103/physrevlett.118.220501